Wednesday, March 25, 2015, 8:30 - Thursday, April 02, 2015, 18:00

Prometheus Hall, 1st floor, KG I, Platz der Universität 3, Freiburg 79098, Germany

The aim of this intensive 8 day course is to give both theoretical background and hands-on practical knowledge in the solution of optimal control problems with underlying differential equation models, as they arise for example in robotics, chemical engineering, biology, mechatronics or aerospace. Participants will learn how to formulate and to numerically solve complex optimal control problems with the help of state-ofthe- art computing tools. Content: The course covers all topics relevant for the formulation and practical solution of optimal control problems (OCP) with nonlinear differential equation models. It starts by recalling concepts from numerical simulation of ordinary differential equation models (ODE) and differential algebraic equations (DAE) as well as concepts from nonlinear optimization with equalities and inequalities, and the computation of derivatives. It then treats the three big families of optimal control solution approaches: the Hamilton Jacobi Bellman (HJB) equation, the indirect approaches based on Pontryagin’s minimum principle, and direct approaches. The major focus of the course is on the latter, in particular on direct collocation, direct single and direct multiple shooting. A second focus is on important application classes such as parameter and state estimation and nonlinear model predictive control (NMPC). The course also treats several implementation and modelling details such as the treatment of higher index DAE and invariants, choice of discretization schemes and quadratic programming (QP) solvers. All lecture topics are accompanied by intensive computer exercises, for which we use the free and open-source optimisation environment CasADi http://casadi.org. In the last three days of the course, the participants will work, during the exercise sessions, on self chosen optimal control problems, whose results will be publicly presented to all course participants on the last day.

Prerequisites, Workload and Evaluation: The course is self contained and can be followed by all quantitative scientists with basic mathematical background (calculus and linear algebra). It is recommended for both industrial and academic practitioners of control and optimization as well as for master and PhD students of engineering, computer science, mathematics, and physics. The total workload is 90 hours including lectures, project work and self-study, and the course gives 3 ECTS credits. The final course evaluation is based 50% on the written exam and 50% on the projects. A certificate of attendance can be given to participants not wishing to participate in the exam and/or project.

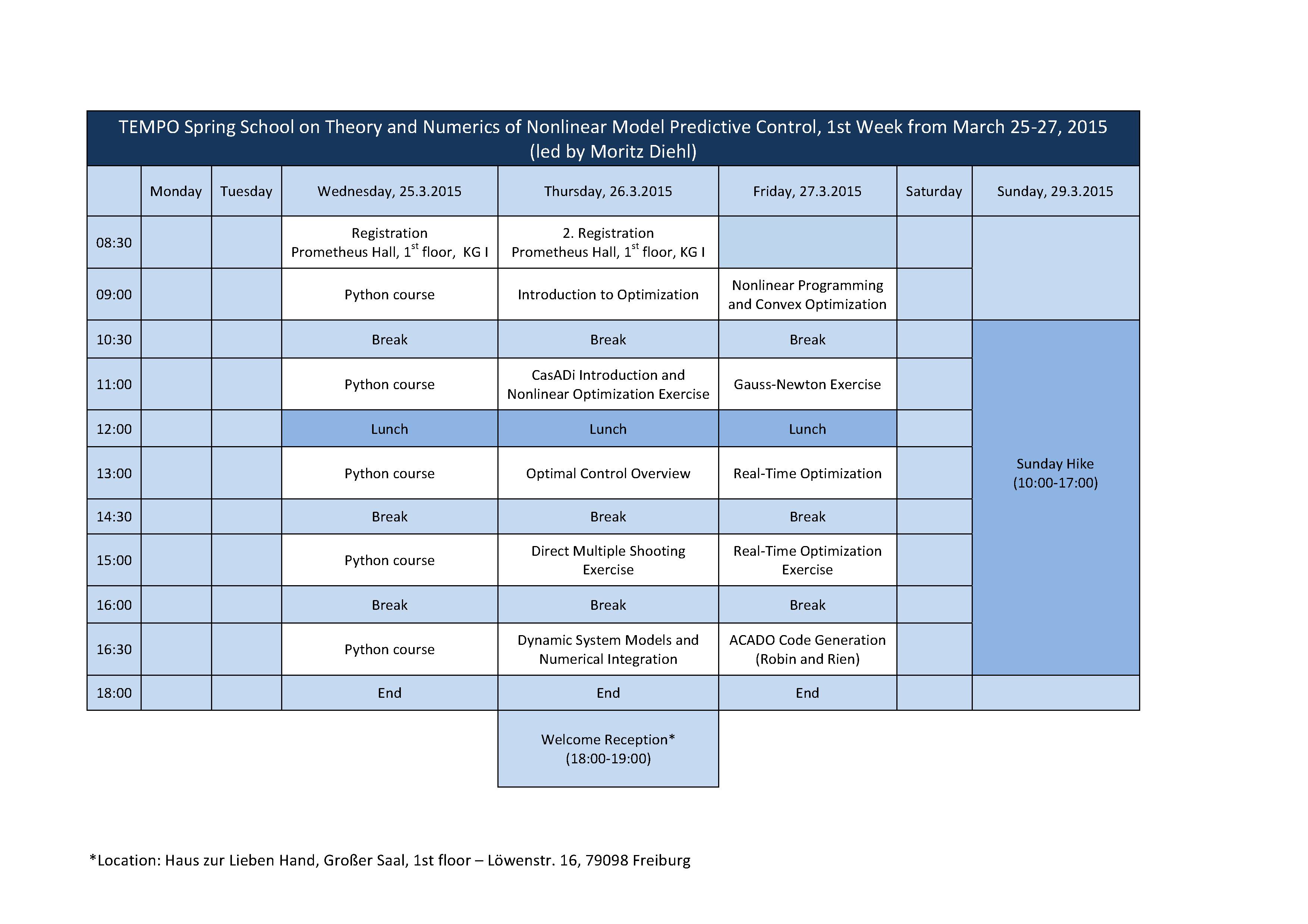
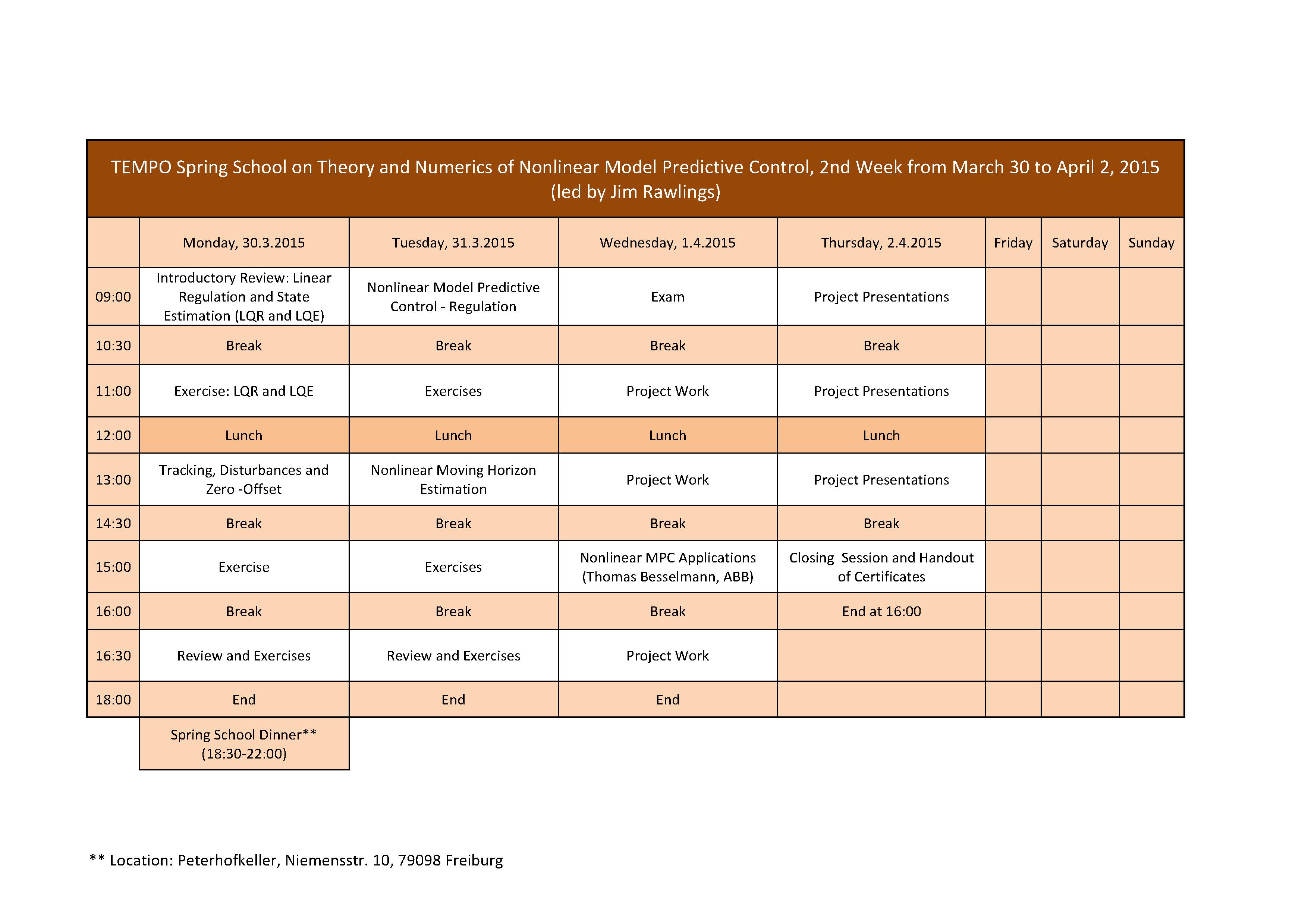
Course schedule

Course material

Welcome Sheet

Program and course information

Python Tutorial

This Python tutorial has been organised to provide you with the basic Python knowledge needed for the rest of the course. You can download the slides, exercise sheets and cheat sheet here.

First Week: Optimization, Optimal Control and NMPC with CasADi

Thursday, March 26, 2015

09:00 – NMPC Spring School Introduction, Optimization Overview
11:00 – Exercise 1: Nonlinear Programming, Solution of Exercise 1
13:00 – Dynamic System Models, Optimal Control Overview
15:00 – Exercise 2: Direct Multiple Shooting, Solution of Exercise 2

Friday, March 27, 2015

09:00 – Constrained Optimization, SQP and IP Methods, (extra: Unconstrained Optimization)
11:00 – Exercise 3: Gauss-Newton SQP, Solution of Exercise 3
15:00 – Integrators and Collocation (extra: Simulation Methods),  Nonlinear MPC (extra: Convexity in Optimal Control), Introduction to ACADO, ACADO demo
16:00 – Exercise 4: Model predictive control, Python code, Tutorial on structures in casadi, Solution of Exercise 4

Extra material:

Social Event: Hike in the Black Forest

Hike information

Second Week

Week 2 website
Exercise 6: Python file cstr.py, Solution of the first part, Solution of Exercise 6
Exercise 8, Python template, Solution of Exercise 8, Solution of Exercise 8 using SX structure
Talk on Nonlinear MPC applications by Thomas Besselmann.

Projects

Please fill in the following project spreadsheet.

Please upload your projects in this Google Drive folder.

Videos (to download, please use “save link as”)

March 25th:
Lecture 1
Lecture 2
Exercise 1
Exercise 2
Exercise Comments

March 26th:
Lecture 1
Lecture 2
Lecture 3
Exercise

March 27th:
Lecture 1
Lecture 2
Lecture 3
Exercise 1
Exercise 2
Exercise 3

March 30th:
Lecture 1
Lecture 2
Lecture 3
Exercise 1
Exercise 2
Exercise 3

March 31th:
Lecture 1
Lecture 2
Lecture 3
Exercise 1
Exercise 2
Exercise 3

April 1st:
Guest Lecture

Recommended books, scripts, and other links

• Book “Model Predictive Control” by J. Rawlings and D. Mayne
• Lecture Notes on “Optimal Control and Estimation” by M. Diehl
• J. Andersson: A General-Purpose Software Framework for Dynamic Optimization. PhD thesis, KU Leuven.
• Bryson, A., and Ho, Y. Applied optimal control: optimization, estimation, and control. Blaisdell, Waltham, MA, 1969.
• Biegler, L. T. Nonlinear Programming. MOS-SIAM Series on Optimization. SIAM, 2010.
• Betts, J. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 2nd ed. SIAM, 2010.